Kayıp enstrümanlarını bulma şansı oldukça düşük olan müzik grubu üyelerini konsere çıkarabilmek için en iyi çözümü bulman gerekecek. Bu bilmeceyi çözebilmek için stratejik zeka ve taktiksel düşünme becerilerini harekete geçirmelisin.
Bu bilmece, binlerce hayranı olan bir müzik grubu ile menajerleri arasında geçiyor. Müzik grubunun üyeleri o kadar dağınık ve düzensiz ki menajerleri bir gün bu durumdan bıkıyor ve onlara büyük bir ders vermek istiyor.
Grup üyeleri kendilerine hazırlanan bilmecede enstrümanlarını bulmaya çalışıyor, ancak olasılık son derece düşük. Bilmeceyi çözebilmek için stratejik düşünmeli ve her adımı dikkatle değerlendirmelisin.
Bir müzik grubu var, müthiş çalıyorlar ama organize olma konusunda berbatlar.

Grup üyeleri tura çıktıklarında enstrümanları hep alakasız yerlere koyuyor ve ortaya çıkan karmaşa, menajerlerini her seferinde cinnetlik duruma getiriyor.
Bir gün en büyük konserlerinden birine çıkmak üzereler, grup bir anda kendini kulis yerine penceresiz ve ses geçirmez bir stüdyoda buluyor. Hem de elleri bağlanmış halde.

Meğer menajerleri grup üyelerine bir ders vermek istemiş. Bütün olay burada başlıyor.

Grubun menajeri bu garip durumu şöyle açıklıyor: Grup üyeleri eğer organize olmayı öğrenemezlerse bütün anlaşmalar iptal. Ne bu konsere ne de gelecek konserlerine çıkamazlar.
Dışarıda 10 büyük kutu var, her birinde grubun 10 üyesinden birinin enstrümanı var, kutuların üzerlerinde de enstrüman resimleri var. Ama bu resimler kutuların içinde ne olduğuna göre değil rastgele yerleştirilmiş.
Menajer, her üyeye birer birer izin vereceğini ve her birinin beş kutunun içine bakabileceklerini söylüyor.

Enstrümanlara dokunamaz ya da hangi kutuda ne bulduklarını diğerlerine söyleyemezler. Kutuları işaretleyemez, arkadaşlarına bilgi veremez, gizli gizli işaretler yaparak ne gördüklerini anlatamazlar.
Her biri kendi enstrümanını bulmayı başarırsa bu geceki konsere çıkabilirler. Yoksa hem menajerleri hem de şirketleri onlarla çalışmayı bırakacak, konser de iptal olacak.
Başlamadan önce düşünmek ve plan yapmak için 3 dakikaları var.
Grup umutsuz bir halde. Şansları inanılmaz düşük.

Her müzisyenin rastgele beş tane kutu seçerek enstrümanlarını bulma şansı %50. Ancak üyelerin hepsinin aynı anda başarılı olma şansı daha da düşük, 1024’te 1.
Ama bir anda davulcunun aklına başarılı olma şansı %35‘ten de yüksek bir fikir geliyor. Bu planın ne olduğunu bulabilir misin?
Cevabı öğrenmeye hazırsan aşağıya bakabilirsin.

Davulcunun planı şu: Herkes ilk olarak kendi enstrümanının resmi olan kutuyu açacak. Eğer enstrüman içerideyse zaten sorun yok. Başardı.
Değilse içeride ne olduğuna bakacak ve sonra içeridekinin resmi olan kutuyu açacak. Enstrümanını bulana kadar böyle devam edecek. Böylece rastgele bir sıra ile gitmeye kıyasla başarı ihtimali ciddi ölçüde artmış olacak.
Olasılık hesabına göre bu plan kusursuz çalışacak ve tüm enstrümanları bulmayı başaran grup üyeleri birkaç saat sonra binlerce hayranının karşısında konser veriyor olacak.
Peki bu plan tam olarak nasıl çalışıyor? Buradan itibaren matematik nerd’leri kulaklarını iyi açsın.

Herkes önce üzerinde kendi enstrümanın resmi olan kutuyu, sonra açtığı kutunun içindeki enstrümanın resminin olduğu, sonra yeni açtığı kutunun içindeki enstrümanın resminin olduğu kutuyu açacak ve bu böyle devam ettiğinde bu sıra bir noktada başa dönmüş olacak.
Bu sistem rastgele tahmin etmekten çok daha iyi çalışır. Çünkü her bir müzisyen, üzerinde kendi enstrümanının resmi olan kutuyla başladığında kendini belirli bir döngüyle kısıtlamış olur.
Peki bu olasılıkları nasıl hesaplarız?
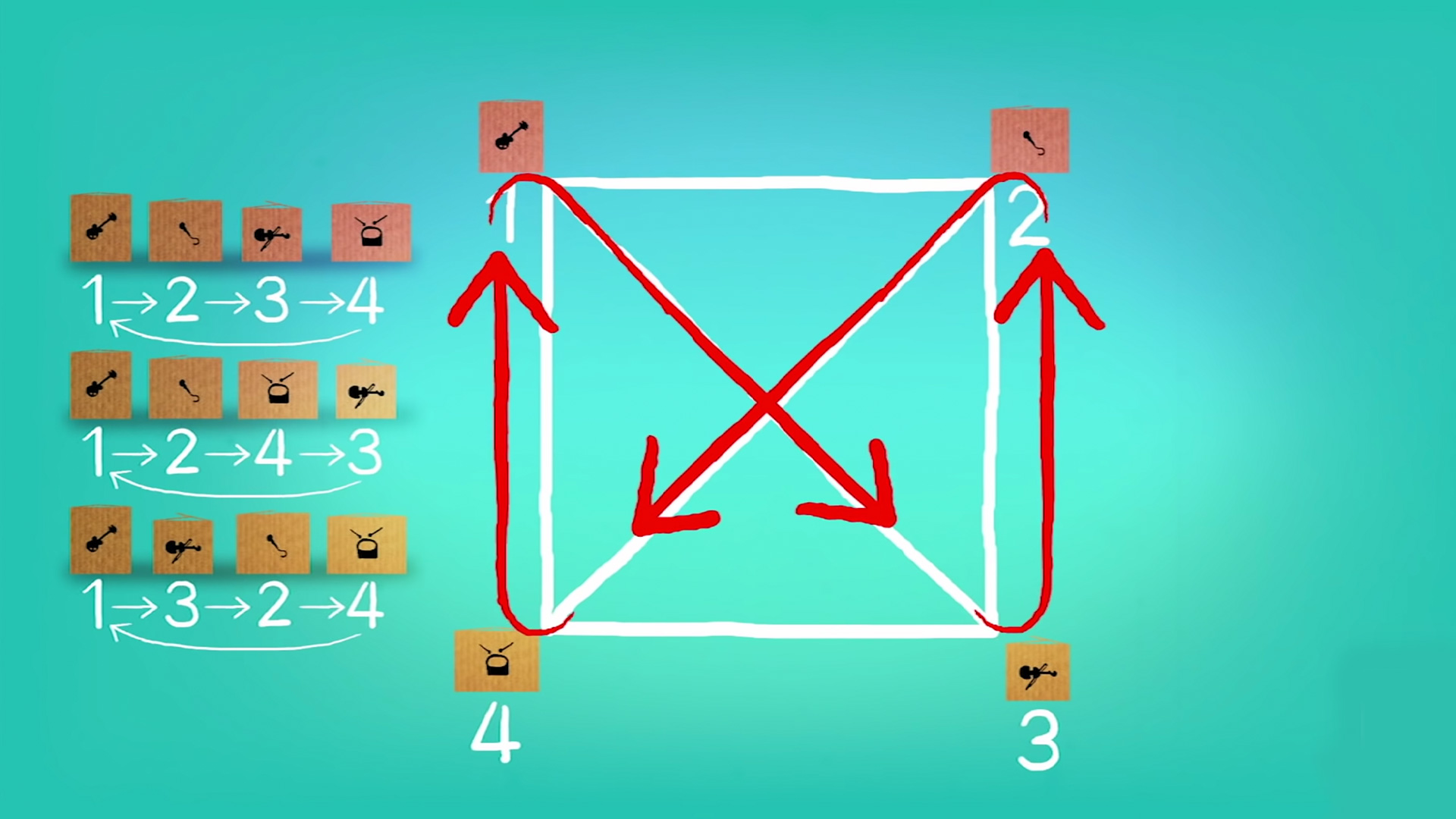
Bunu anlamak için elimizdeki bilmeceden biraz daha basit bir senaryo düşünelim, sadece 4 enstrüman ve her müzisyen için 2 seçme hakkı olsun.
Her bir müzisyenin başarısız olma ihtimallerinin ne olduğuna bakalım. Başarısız olması için aradığını, ilk ya da ikinci seferde değil, üçüncü ya da dördüncü seferde bulması gerekir. Önünde 4 kutu içinde 6 farklı şekilde seçim yapma ihtimali var demektir.
Bunu daha iyi anlamanın bir yolu bir kare çizmek, her bir köşeye bir enstrümanı yerleştirip karşı köşeleri birleştirmek.

Böylece bu çizgiler üzerinde kaç farklı yol çizebileceğinizi görebilirsiniz.
Unutma ki hangi köşeden başlarsa başlasın ok bu şekilde aynı yönde devam ettiği sürece birbirinin aynısı sayılır. Ama bu aşağıdaki ikisi birbirlerinden farklı.
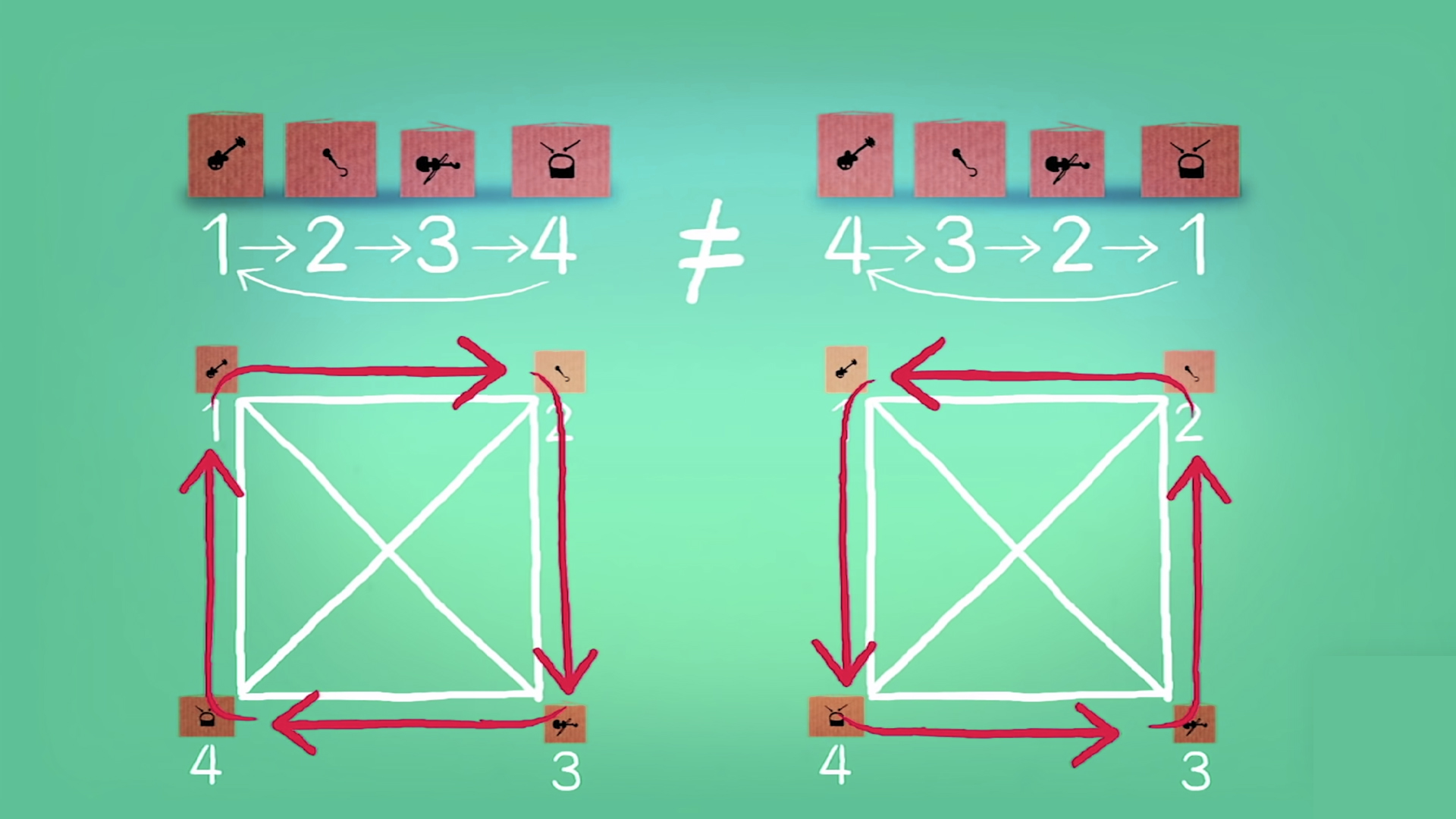
Burada üçgen şeklini alan sekiz farklı üçlü döngü görebiliriz. Kare, yani dörtlü seçim yerine üçgen yani üçlü seçim şeklinde ilerlediğinizde hangi enstrümanın dışarıda kaldığna göre dört tane üçgen ve iki farklı yol görürsünüz.
24 olası kutu kombinasyonundan 14 tanesi sizi başarısızlığa, 10 tanesi başarıya ulaştırır.
Bu hesap yöntemi, müzisyen sayısı çift sayı olduğunda her zaman çok iyi çalışır.
Daha kısa ve teknik bir yoldan anlatmak gerekirse karşımıza şöyle bir denklem çıkar.
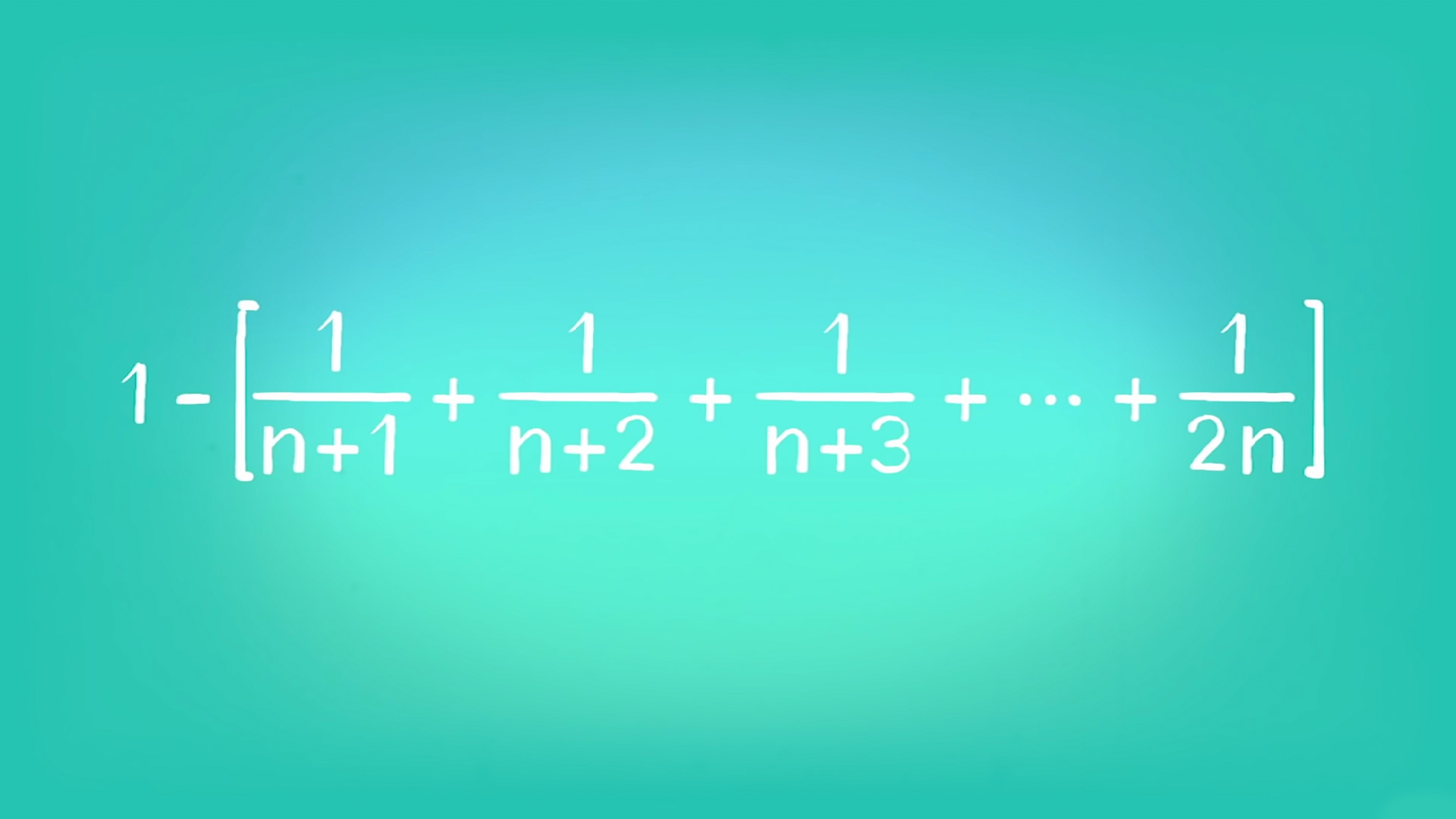
10 müzisyen olduğunda olasılık %35 civarı çıkıyor.
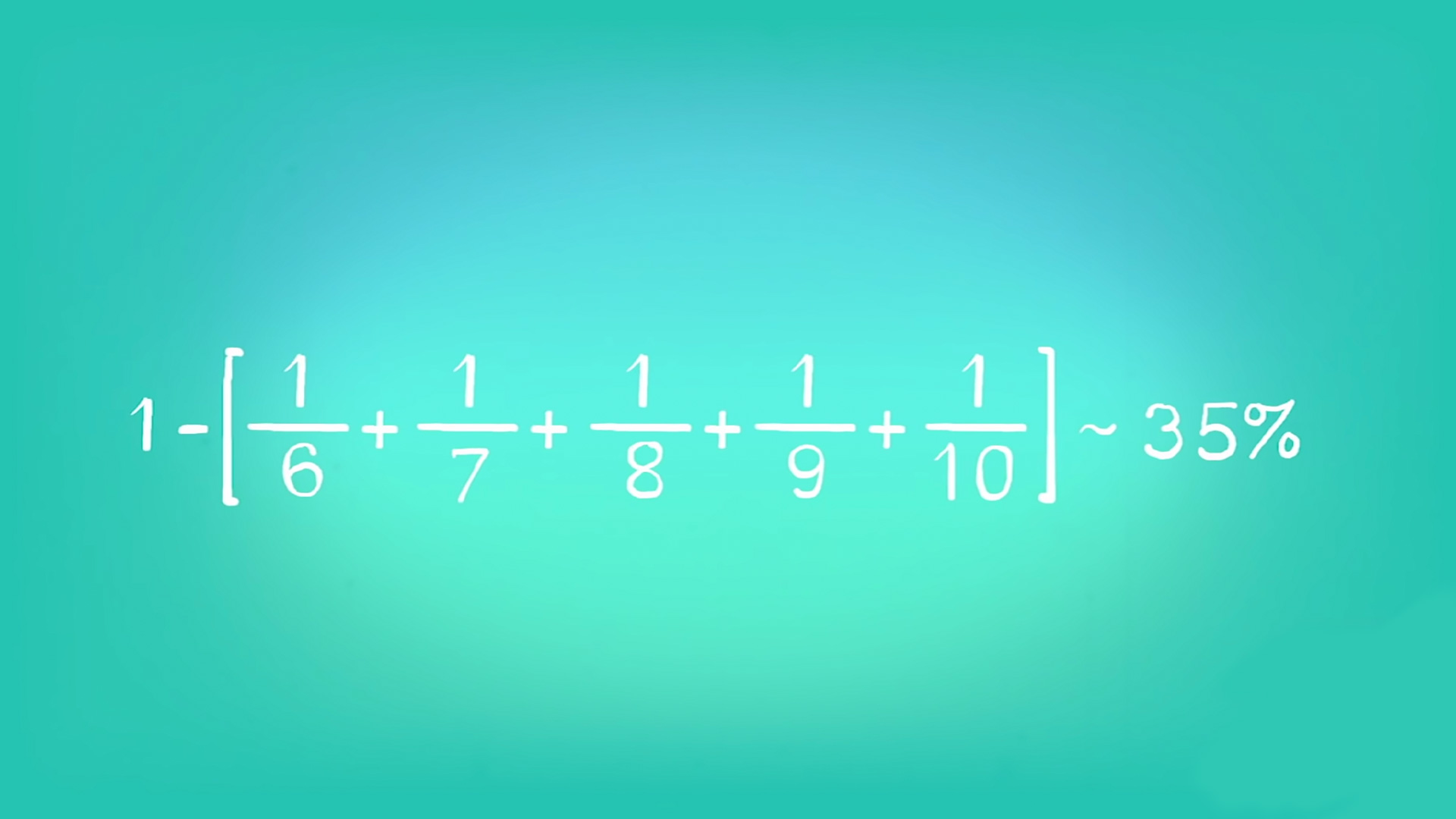
Peki 1000 müzisyen olsa, hatta 1.000.000?
Bu denklemdeki n sayıları, yani müzisyen ve ekipmanlar arttıkça olasılık yaklaşık %30’a yaklaşır.
Yani sonuç garanti değil, ama müzisyenlerin şanslarını inanılmaz derecede artıran bir çözüm.
Sonuç olarak 1024’te 1 nerede, %35 nerede…
