İkinci dereceden denklemler konusunun bir alt başlığı olan parabol, günümüzde birçok öğrenci tarafından pek sevilen ve anlaşılabilen bir konu değil. Biz de bu arkadaşlara parabolü sevdirmek adına, konu anlatımı yaparak denklemler üzerinden çeşitli örnek sorular çözdük.
Tarihi M.Ö. 380’li yıllara kadar dayanan parabol, her zaman matematiğin en dikkat çeken alanlarından biri olmuştur. Diğer konulardan farklı olarak parabol icat edilmedi. Aksine keşfedildi ve üzerinde çeşitli araştırmalar yapıldı. Günümüzde birçok pratik uygulamada kullanılıyor.
Bu yazımızda da, parabolü tüm detaylarıyla ele alarak konu anlatımı yaptık. Ayrıca, konuyu pekiştirmek adına sık kullanılan denklemleri kullanarak daha önce sınavlarda çıkmış örnek soruları çözdük. Lafı daha fazla uzatmadan içeriğimize geçelim.
Temelden başlayalım; parabol nedir?
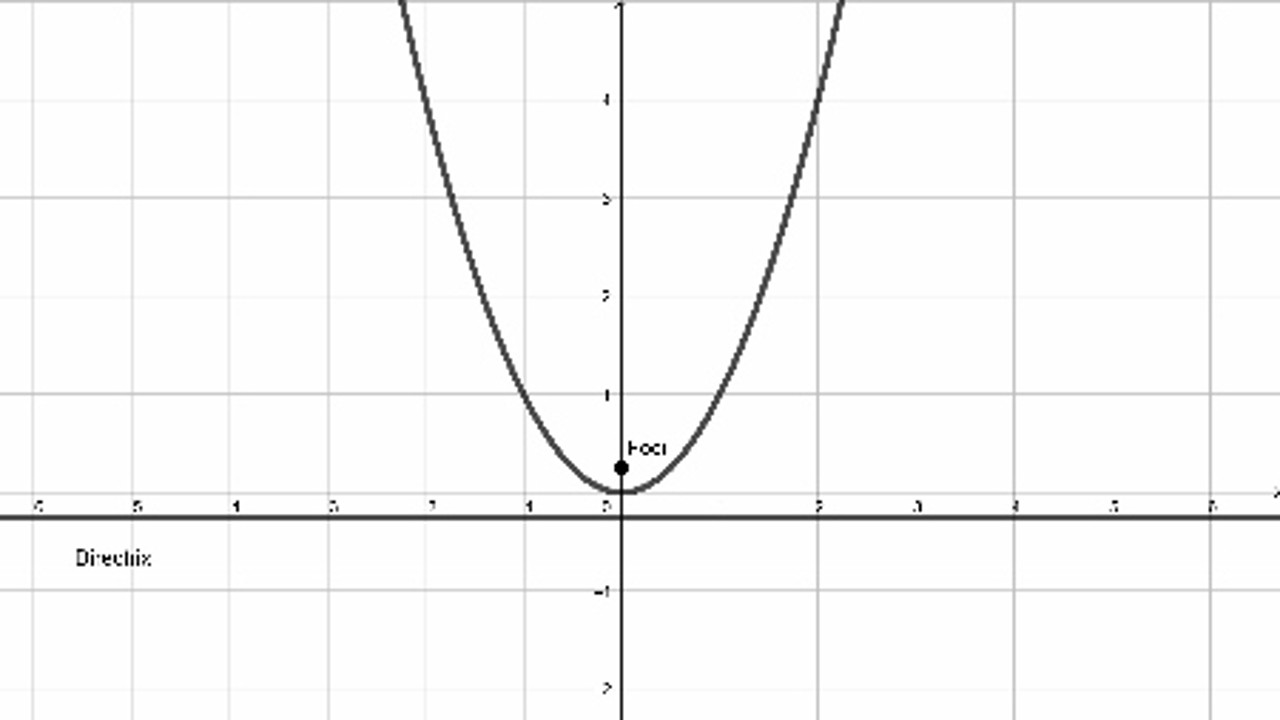
Parabol, kısaca belirli bir eğrinin denklemidir; öyle ki, eğri üzerinde bulunan her nokta, sabit bir noktadan ve sabit bir çizgiden her zaman eşit uzaklıkta olur. Bu sabit nokta parabolün odak noktasıdır ve sabit çizgi parabolün doğrultmanıdır. Başka bir deyişle, belirli bir noktadan veya belirli bir çizgiden eşit uzaklıkta olan bir noktanın geometrik kısmına parabol denir.
Parabolik eğriler fizik, mühendislik, finans ve bilgisayar bilimleri gibi birçok alanda yaygın olarak kullanılıyor. Parabol, denkleme bağlı olarak yukarı veya aşağı içbükey olabilen U şeklinde bir eğridir.
Peki parabol nasıl ortaya çıktı?

Tarihsel olarak parabolün geometrik özellikleri eski Yunanlılar tarafından ortaya konmuştur. Tarihsel kayıtlar incelendiğinde Menacchmus ( M.Ö. 380-320), hiperbol ve elipsin yanı sora parabolün özelliklerini de inceleyen ilk kişi olarak karşımıza çıkıyor. Daha sonra, Pergeli Apollonius M.Ö. 262-190) konik kesitler üzerine bir çalışma yaptı, fakat yaptığı parabol tanımı oranlar cinsindendi ve çalışmasında herhangi bir koordinat kullanımı yoktu.
Bu tarihlerden uzun yıllar sonra, Galileo (1564-1642), bir merminin yerçekimi etkisi altında parabolik bir yol ile ilerlediğini fark etti. Ünlü matematikçi Kepler (1571-1630) ise, gezegenlerin Güneş etrafında hareket ederken eliptik şekle çok yakın bir şekilde döndüğünü ilk fark eden kişi oldu. Newton ise bunu evrensel çekim yasasını kullanarak kanıtladı.
Parabolün standart denklemi nedir, nasıl yazılır?
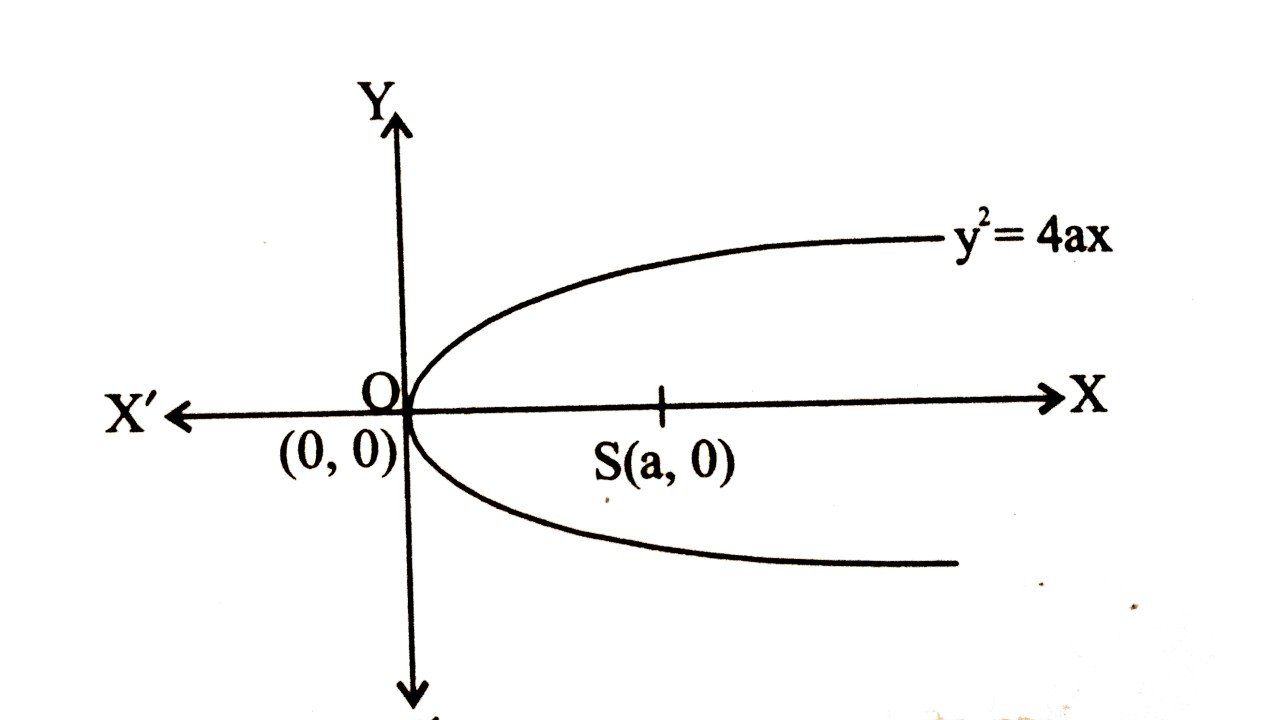
XY düzleminde yer alan parabol üzerinde koordinatları (x,y) olan bir P noktası alın. Parabolün tanımı gereği, parabol üzerindeki herhangi bir noktanın odağa ve doğrultmana olan uzaklığı eşittir. P’nin doğrultmana olan uzaklığı ise PB şeklinde ifade edilir; burada B’nin koordinatları doğrultu üzerinde yer aldığı içim (-a, y)’dir ve P’nin odaktan uzaklığı PF’dir.
Parabol tanımına göre PF = PB (1) olduğundan, uzaklık formülü kullanarak şu sonucu elde ederiz:
PF = √((x-a)² +(y-0)² = √{(x-a)² +y² } . . . .(2)
PB = √{(x+a)² } (3)
(1), (2) ve (3). denklemleri kullanarak şu sonucu elde ederiz:
√{(x−a) +y² } = √{(x+a)² }
⇒ (x-a)² + y² = (x+a)²
⇒ x² + a² – 2ax + y² = x² + a² + 2ax
⇒ y² – 2ax = 2ax
= y² = 4ax
Genel olarak, bir parabolün standart denkleminde doğrultman y eksenine paralel ise şu şekilde bir denklem oluşur;
y² = 4ax
Eğer parabol yan yana ise, yani doğrultman x eksenine paralel ise, parabolün standart denklemi şöyle olur;
x² = 4ay
Bu iki durum dışında bir parabolün denklemi, eğer parabol negatif kısımda ise y² = -4ax ve x² = -4ay şeklinde olabilir.
Parabol formülleri nelerdir?
Tepe noktası ve bir noktası bilinen parabol formülü
y = a.(x-r)² + k
x ekseninin kestiği noktalar ve üzerinde başka bir nokta bilinen parabol formülü
f(x) = a. (x – x1) . (x – x2)
Üç noktası bilinen parabol formülü
y=f(x) =ax² + bx + c
Sınavlarda çıkmış örnek parabol soruları
Soru 1:

Şekilde grafiği verilen parabolün tepe noktası, T(5/2, 5) ve y eksenini kestiği nokta A(0,4)’tür. Bu parabolün denklemi y = ax² + bx + c olduğuna göre b kaçtır?
Çözüm 1:
Tepe noktasını kullanarak,
y = a(x+5/2)² + 5 şeklinde denklemi yazabiliriz.
(0,4) noktasını da kullanalım.
4 = a(0+5/2)² + 5
4 = 25a / 4 + 5
-1 = 25a/4 => -4 = 25a => a = – 4 / 25’tir.
y = – 4 / 25 (x+5/2)² + 5 denklemini açarak yazalım.
= – 4 / 25 x² + 5x + 25/4) + 5
= – 4 /25 x² – 4 / 5 x + olur.
Buna göre b = -⅘ olur.
Soru 2:
y = x² parabolü ile y = 2 – x doğrusu arasında kalan sınırlı bölgenin sınırları üzerindeki (x, y) noktaları için x² + y² ifadesinin alabileceği en büyük değer kaçtır?
Çözüm 2:
ilk önce parabol ile doğrunun grafiğini çizelim. y = x² parabolü tepe noktası orjin olan kolları yukarı doğru olan bir paraboldür. y = 2 – x doğrusu eksenleri 2 ve 2 noktasında keser.
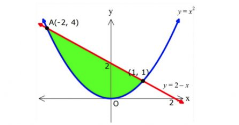
x²+ y²nin en büyük değeri için orjinden en uzak noktayı almalıyız. Bu da A noktasıdır. A noktasının koordinatlarını bulalım.
x²- 2 – x
x² + x – 2 = 0
(x+2)(x-1) = 0 , x = -2 değeri A’nın apsisidir.
x = -2 için y = 2 – x – 4’tür.
A(-2, 4) noktası için
x² + y² = (-2)² + 4²
= 4 + 16 = 20’dir.
Soru 3:
y = x² – 2(a + 1 )x + a² -1
parabolü y = 1 doğrusuna teğet olduğuna göre, a kaçtır?
Çözüm 3:
y = 1 olduğunda fonksiyonun tek bir kökü olmalı ki y = 1 doğrusunda teğet olsun. O halde,
1 = x² – 2(a+1)x + a² -1
0 = x² -2(a +1)x + a² – 2 denkleminde Δ = 0’dır.
(-2(a+1))² – 4.a.(a²-2)=0
4(a² + 2a + 1)- 4a² + 8 = 0
8a + 12 = 0
8a = -12
a= -3/2
Soru 4:
a ve b pozitif gerçel sayılar olmak üzere, dik koordinat düzleminde orijinden geçen
p (x + a) + b
p (x + a) – b
p (x – a) – b
biçiminde tanımlanan üç parabolün tepe noktaları, alanı 16 birimkare olan bir üçgenin köşe noktalarıdır.
Buna göre, a + b toplamı kaçtır?
Çözüm 4:
p (x) = (x-a)² -b polinomu orjinden geçiyorsa, (0,0) noktası parabolün bir noktasıdır.
0 = (0-a)² – b
0 = a² – b => a² = b ‘dir.
Diğer polinomların tepe noktasını bulalım.
p ( x + a) + b = (((x+a)-a)² – b ) + b
=x² – b + b
= x²’dir. Tepe noktası (0,0) noktasıdır.
p ( x + a) -b = (((x-a)-a)² -b ) -b
= x²-b-b
= x² – 2b’dir. Tepe noktası (0,2b) noktasıdır.
p (x-a) -b =(((x-a)-a)² – b ) -b
= (x-2a)² -b -b
= (x-2a)² -2b’dir. Tepe noktası (2a, -2b) noktasıdır.
Koordinat düzleminde inceleyelim.
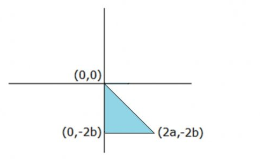
Taban kısmı 2a uuzunlukta, yüksekliği ise 2b uzunluğunda olan bir üçgen elde ediliyor. Bu üçgenin alanı ise 16br² ise,
(2b.2a)/2 = 16
ab = 8’dir.
a² = b ise a = 2’dir.
b = a² = 4’tür.
a + b = 2+4 = 6
Soru 5:

f(x) fonksiyonunun grafiği, şekildeki gibi, Ox eksenine (1, 0) noktasında teğet olan ve (0, 3) noktasından geçen paraboldür.
Buna göre, f(3) kaçtır?
Çözüm 5:
Tepe noktası (1, 0) noktası ise
y = a(x-1)² + 0 denklemi ortaya çıkar.
(0, 3) noktasından geçtiğini kabul edersek,
3 = a(0-1)²
3 = a.1 => a = 3
f(x) = 3(x-1)² ise f(3)=3.(3-1)² = 3.4 = 12’dir.
